6.2.10.2.3 Ich sehe einfach nicht, welche logische Identität ich anwenden soll

Ich sehe einfach nicht, welche logische Identität ich anwenden soll

Ein Student schrieb mir (sinngemäß):

Frage

Ich sehe es einfach nicht.
Welche logische Identität soll ich denn anwenden?

Und in der Tat ist das am Anfang ein schwieriges Problem. Es wird aber einfacher, je mehr Übung man hat. Es geht um Aufgaben dieses Typs:

Aufgabe

 Aufg. 50: Vereinfache mit logischen Identitäten!

Vereinfache den folgenden Term unter Anwendung von logischen Identitäten soweit wie möglich:

$(A\land B)\rightarrow \neg (A\lor (B\land C))$

Die ersten Orientierungsschritte

Das folgende Vorgehen beschreibt einen möglichen Weg, auch wenn dieses nicht immer den kürzesten Weg zum Ziel ergibt.

Schritt 1

Du musst dich mit der Bindungsstärke auskennen!

Falls das bei dir nicht der Fall ist, lies nochmal diesen Abschnitt:
Die Sache mit der Bindungsstärke und bearbeite die Aufgabe dort.

Schritt 2

Du musst die "einfachen Gesetze" kennen! Wende sie bei jeder Gelegenheit an!

Gemeint sind hier:

• Doppelnegationsgesetz
• Neutralitätsgesetze
• Extremalgesetze
• Idempotenzgesetze
• Komplementärgesetze

Die "einfachen Gesetze" sind nicht schwer, und sie verkürzen sofort den Term. Meist können Sie im Verlauf von Schritt 5 angewendet werden.

Schritt 3

Ersetze alle Implikationen und Äquivalenzen (sofern vorhanden).

Du erhältst damit einen Term, der als Junktoren nur noch die Negation, das logische UND sowie das logische ODER enthält.

Die für diesen Schritt notwendigen logischen Identitäten findest du im Absatz:
Weitere logische Identitäten

Beispiel

Hier wird eine Implikation durch die Anwendung der entsprechenden logischen Identität aufgelöst:

${\begin{aligned}&(A\land B)\rightarrow \neg (A\lor (B\land C))\\[.2cm]\equiv \quad &\neg (A\land B)\lor \neg (A\lor (B\land C))\end{aligned}}$

Schritt 4

Solange es eine Negation vor einer Klammer gibt, wende "De Morgan" an.

Beispiel

Hier gibt es zwei Klammern mit einer Negation davor. Also wird auch "De Morgan" (mindestens) zweimal angewandt:

${\begin{aligned}&\neg (A\land B)\lor \neg (A\lor (B\land C))\\[.2cm]\equiv \quad &(\neg A\lor \neg B)\lor \neg (A\lor (B\land C))\end{aligned}}$

Weil du dich ja mit der Bindungsstärke auskennst ist dir klar, dass du die ersten Klammern weglassen kannst:

${\begin{aligned}\equiv \quad &\neg A\lor \neg B\lor \neg (A\lor (B\land C))\end{aligned}}$

Jetzt die zweite Anwendung von "De Morgan":

${\begin{aligned}\equiv \quad &\neg A\lor \neg B\lor \neg A\land \neg (B\land C)\end{aligned}}$

Hier kann "De Morgan" auch noch ein drittes mal angewendet werden:

${\begin{aligned}\equiv \quad &\neg A\lor \neg B\lor \neg A\land (\neg B\lor \neg C)\end{aligned}}$

Dir ist klar, warum die Klammern am Ende bleiben müssen?
Falls nein: Zurück zu Schritt 1.

Schritt 5

Wende die Absorptionsgesetze und die Distributivgesetze an.

Leider gibt es in diesem Schritt nicht immer sofort die Möglichkeit, die Absorptionsgesetze anzuwenden. Falls es möglich ist, erhältst du umgehend einen deutlich kürzeren Term:

Beispiel

   

Dir ist klar, warum der große gelbe Bereich am Ende zusammen gehört?
Falls nein: Zurück zu Schritt 1.

${\begin{aligned}\equiv \quad &\neg A\lor \neg B\end{aligned}}$

Das Absorptionsgesetz hat den großen gelben Bereich am Ende absorbiert.

Stillschweigend wurde hier auch das Kommutativgesetz angewendet (direkt vor dem Absorptionsgesetz).

Falls eine Anwendung der Absorptionsgesetze nicht möglich ist, wende die Distributivgesetze an. Und denke an Schritt 2!

Mach' einfach was!

Wichtig

Am Anfang, wenn du noch "kein Auge" für die logischen Identitäten hast, ist wichtig: Mach' einfach was! Wende logische Identitäten an!

Es wurde schon mehrfach darauf hingewiesen, dass es verschiedene Wege zum Ziel (also zur einfachsten Gestalt des Terms) gibt. Den kürzesten Weg findet man nur selten. Aber jeder andere (korrekte!) Weg ist legitim und bringt beim Lösen einer Aufgabe die volle Punktzahl.

An dieser Stelle folgt üblicherweise folgende Frage:

Frage

Wenn ich eine logische Identität anwende, dann weiss ich gar nicht, ob ich das überhaupt richtig gemacht habe. Wie kann ich das prüfen?

Wenn du eine Lerngruppe hast (und ich empfehle dir sehr, dass du eine Lerngruppe hast), dann kann jedes Mitglied der Gruppe die Aufgabe separat rechnen. Am Ende werden die Ergebnisse verglichen.

Falls es mehrere unterschiedliche Ergebnisse gibt, kann anhand von Wahrheitstafeln geprüft werden, welches Ergebnis korrekt ist.

Wenn dein Ergebnis richtig ist: Prima! Du bist auf einem guten Weg!

Wenn du einen Fehler gemacht hast: Auch prima! Denn aus Fehlern wird man klug (drum ist einer nicht genug, sagt der Volksmund). Du musst jetzt nur noch den Fehler finden, deine Lerngruppe kann dir dabei helfen.

"Aber in meiner Lerngruppe kennt sich niemand mit den logischen Identitäten aus!" Auch diesen Satz höre ich nicht zum ersten mal.

Jetzt hilft dir (und deiner Lerngruppe) das Internet weiter.

Logik-Rechner im Internet

Schau mal auf diese Webseite mit einem Logik-Rechner:
http://www.elektroniker-bu.de/boolesche.htm

Du kannst hier einen aussagenlogischen Term eingeben (--> Boolescher Ausdruck), allerdings musst du dich erst mit der dort vorausgesetzten Eingabesyntax vertraut machen. (Die Syntax wird direkt auf der Seite erklärt.)

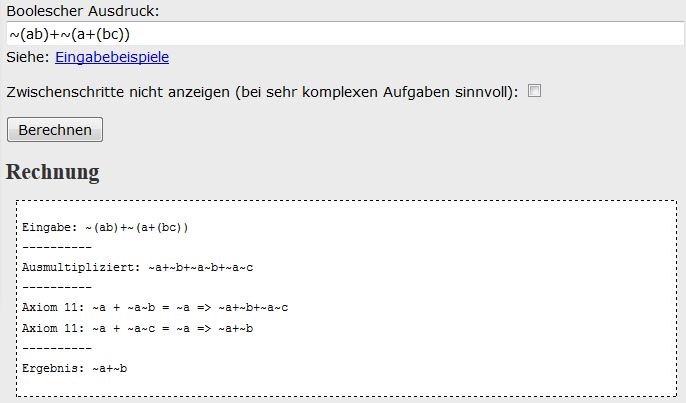
Unser Beispiel von oben (die Implikation muss schon umgewandelt sein)

$\neg (A\land B)\lor \neg (A\lor (B\land C))$

wird hier notiert als

    ~(ab)+~(a+(bc))

Anschließend genügt ein Klick auf "Berechnen" und das Ergebnis erscheint.

Wieder eine typische Frage an dieser Stelle:

Frage

Darf ich den Logik-Rechner auch in der Klausur einsetzen?

Du kennst die Antwort.

Wie kann ich den Logik-Rechner zum Lernen verwenden?

Sobald der Logik-Rechner das Ergebnis berechnet hat, erscheint der Rechenweg. Diesen musst du nachvollziehen!

Üblicherweise wird zunächst "ausmultipliziert", anschließend werden verschiedene "Axiome" angewandt. Wenn du herausfindest, welche logischen Identitäten hinter dem Ausmultiplizieren und den Axiomen stecken, dann hast du etwas gelernt.

Denk' dir aussagenlogische Terme aus!

Mit etwas Phantasie kannst du (und jeder andere in deiner Lerngruppe) in der Folge eigene aussagenlogische Terme notieren (Denk' dir was aus!). Dann empfehle ich diese Vorgehensweise:

• Anfangs lässt du den Logik-Rechner das Ergebnis berechnen und vollziehst es nach. So baust du Erfahrung auf.

• Später berechnest du erst das Ergebnis selbst und überprüfst es anschließend mit Hilfe des Logik-Rechners. Bei Abweichungen suchst du deinen Fehler und bist wieder etwas schlauer geworden.

Hinweis

Die Vergangenheit hat gezeigt: Einige Studierende begnügen sich mit Punkt 1: Lass den Logik-Rechner mal machen! Auch die offiziellen Einsendeaufgaben für das Studium lassen sich so ja bequem lösen.

Falls du auch zu denjenigen gehörst, die großzügig auf die Anwendung von Punkt 2 verzichten, so wünsche ich dir "viel Glück" in der Klausur. Du wirst wirklich viel davon brauchen.