6.2.9.1 Beweisführung anhand einer Wahrheitstafel
| [unmarkierte Version] | [gesichtete Version] |
Keine Bearbeitungszusammenfassung |
LOOP2 Upgrade |
||
| (6 dazwischenliegende Versionen von einem anderen Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
=Beweisführung anhand einer Wahrheitstafel= | =Beweisführung anhand einer Wahrheitstafel= | ||
<p> | |||
Eine Aufgabe und deren Lösung: | |||
</p> | |||
<loop_area type="task"> | |||
Beweise mit Hilfe einer Wahrheitstafel:<br /> | |||
:<math> | |||
(A \leftrightarrow B) \; \equiv \; (A \rightarrow B) \land (B \rightarrow A) | |||
</math> | |||
</loop_area> | |||
<br /> | |||
<p> | |||
Das folgende Video zeigt die Beweisführung: | |||
</p> | |||
<loop_media type="video" title="Beweis der Äquivalenz bei logischen Identitäten" description="http://youtu.be/vcklrdE8sKs" copyright="CC-BY" index=true show_copyright=true id="5fa958f9c157d"> | |||
{{#ev:youtube|vcklrdE8sKs|700}} | |||
</loop_media> | |||
<br /> | |||
<p> | |||
Hier ist die im Video erstellte Wahrheitstafel: | |||
</p> | |||
<p class="autoitprint"> | |||
[[File:beweis-mit-wahrheitstafel.jpg|beweis-mit-wahrheitstafel.jpg]] | |||
</p> | |||
<p> | |||
Da beide gelb markierten Spalten identische Werte in den jeweiligen Zeilen aufweisen, ist die Äquivalenz bewiesen. (Unter der Voraussetzung, dass die ermittelten Werte in der Wahrheitstafel korrekt sind.) | |||
</p> | |||
<br /> | |||
<div class="clearer"></div> | |||
<p> | |||
Jetzt bis du dran: | |||
</p> | |||
<br /> | |||
=== Aufgabe 1 === | |||
<loop_area type="task"> | |||
<loop_task title="Beweise mit Hilfe einer Wahrheitstafel!" id="5fa958f9c1585"> | |||
<p> | |||
:<math> | |||
( \neg A \land B ) \lor A \; \equiv \; ( B \lor A ) | |||
</math> | |||
</p> | |||
</loop_task> | |||
</loop_area> | |||
<br /> | |||
=== Aufgabe 2 === | |||
<loop_area type="task"> | |||
<loop_task title="Beweise mit Hilfe einer Wahrheitstafel!" id="5fa958f9c158a"> | |||
<p> | |||
:<math> | |||
( \neg A \lor B ) \land A \; \equiv \; ( B \land A ) | |||
</math> | |||
</p> | |||
</loop_task> | |||
</loop_area> | |||
<br /> | |||
=== Aufgabe 3 === | |||
<loop_area type="task"> | |||
<loop_task title="Beweise mit Hilfe einer Wahrheitstafel!" id="5fa958f9c158f"> | |||
<p> | |||
:<math> | |||
( A \land B ) \lor (A \land \neg B) \; \equiv \; A | |||
</math> | |||
</p> | |||
</loop_task> | |||
</loop_area> | |||
<br /> | |||
=== Aufgabe 4 === | |||
<loop_area type="task"> | |||
<loop_task title="Beweise mit Hilfe einer Wahrheitstafel!" id="5fa958f9c1595"> | |||
<p> | |||
:<math> | |||
( A \lor B ) \land (A \lor \neg B) \; \equiv \; A | |||
</math> | |||
</p> | |||
</loop_task> | |||
</loop_area> | |||
<br /> | |||
=== Aufgabe 5 === | |||
<loop_area type="task"> | |||
<loop_task title="Beweise mit Hilfe einer Wahrheitstafel!" id="5fa958f9c159a"> | |||
<p> | |||
:<math> | |||
( A \rightarrow B ) \land \neg B) \rightarrow \neg A \; \equiv \; 1 | |||
</math> | |||
<spoiler text="Hinweis"> | |||
<p> | |||
Wenn der Term <math>( A \rightarrow B ) \land \neg B) \rightarrow \neg A</math> äquivalent zu <math>1</math> ist, dann muss für diesen Term jede Zeile der Wahrheitstafel zu <math>1</math> werden. | |||
</p> | |||
</spoiler> | |||
</p> | |||
</loop_task> | |||
</loop_area> | |||
<br /> | |||
=== Aufgabe 6 === | |||
<loop_area type="task"> | |||
<loop_task title="Beweise mit Hilfe einer Wahrheitstafel!" id="5fa958f9c159e"> | |||
<p> | |||
:<math> | |||
(\neg A \rightarrow B) \rightarrow \neg (\neg A \rightarrow \neg B) \; \equiv \; \neg A | |||
</math> | |||
</p> | |||
</loop_task> | |||
</loop_area> | |||
<br /> | |||
=== Aufgabe 7 === | |||
<loop_area type="task"> | |||
<loop_task title="Beweise mit Hilfe einer Wahrheitstafel!" id="5fa958f9c15a3"> | |||
<p> | |||
:<math> | |||
((\neg A \lor C ) \land (B \lor \neg C)) \rightarrow ((B \lor C) \rightarrow (A \land C)) \; \equiv \; A \lor \neg B | |||
</math> | |||
</p> | |||
</loop_task> | |||
</loop_area> | |||
<br /> | |||
Aktuelle Version vom 9. November 2020, 15:58 Uhr
Beweisführung anhand einer Wahrheitstafel
Eine Aufgabe und deren Lösung:
Aufgabe
Beweise mit Hilfe einer Wahrheitstafel:
Das folgende Video zeigt die Beweisführung:
Hier ist die im Video erstellte Wahrheitstafel:
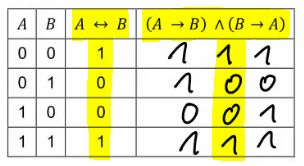
Da beide gelb markierten Spalten identische Werte in den jeweiligen Zeilen aufweisen, ist die Äquivalenz bewiesen. (Unter der Voraussetzung, dass die ermittelten Werte in der Wahrheitstafel korrekt sind.)
Jetzt bis du dran:
Aufgabe 1
Aufgabe
Aufgabe 2
Aufgabe
Aufgabe 3
Aufgabe
Aufgabe 4
Aufgabe
Aufgabe 5
Aufgabe
Aufgabe 6
Aufgabe
Aufgabe 7
Aufgabe