Die einfachste Gestalt durch ein KV-Diagramm ermitteln

Die einfachste Gestalt durch ein KV-Diagramm ermitteln

Das Karnaugh-Veitch-Diagramm (kurz KV-Diagramm) ist ein einfaches Hilfsmittel zur schnellen Ermittlung eines minimalen logischen Ausdrucks aus einer gegebenen Booleschen Funktion.

Genauer benötigt man die Werte aus der Ergebnisspalte einer Wahrheitstafel und ordnet Sie in einem KV-Diagramm neu an.

Hinweis

KV-Diagramme gehören nicht zum offiziellen Lernstoff des Moduls "Lineare Algebra" an der Hochschule Emden/Leer. Aus diesem Grund werden KV-Diagramme an dieser Stelle nur sehr vage und anhand eines einzelnen Beispiels beschrieben.

Insgesamt bieten KV-Diagramme noch sehr viel mehr Möglichkeiten, als auf dieser Seite gezeigt. Wikipedia bietet bei Bedarf weitere Informationen:
http://de.wikipedia.org/wiki/Karnaugh-Veitch-Diagramm

Wieder der Reihe nach:

Gegeben war dieser aussagenlogische Term:

$((A\to B)\to (B\to C))\to C$

Dazu wurde die Wahrheitstafel notiert und die Ergebnisspalte berechnet:

$A$	$B$	$C$	$((A\to B)\to (B\to C))\to C$
$0$	$0$	$0$	$0$
$0$	$0$	$1$	$1$
$0$	$1$	$0$	$1$
$0$	$1$	$1$	$1$
$1$	$0$	$0$	$0$
$1$	$0$	$1$	$1$
$1$	$1$	$0$	$1$
$1$	$1$	$1$	$1$

Der weitere Ablauf unter Zuhilfenahme eines KV-Diagramms ist wie folgt:

Zunächst zeichnet man die Umrisse des KV-Diagramms. Da wir in diesem Beispiel acht Werte in der Ergebnisspalte der Wahrheitstafel haben, ordnen wir zwei Zeilen zu je vier Spalten an:

Die Zeilen und Spalten werden geeignet beschriftet:

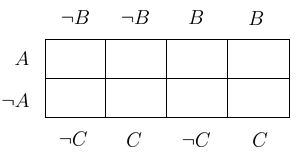
Die geeignete Beschriftung ist hier sehr wichtig. Man erkennt:

• In der ersten Zeile gilt $A$.
• In der zweiten Zeile gilt $\mathrm{\neg }A$.
• In der ersten und zweiten Spalte gilt $\mathrm{\neg }B$.
• In der dritten und vierten Spalte gilt $B$.
• In der ersten und dritten Spalte gilt $\mathrm{\neg }C$.
• In der zweiten und vierten Spalte gilt $C$.

Die acht Werte aus der Ergebnisspalte der Wahrheitstafel werden an die richtige Stelle in das Diagramm geschrieben.

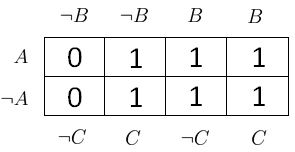
Aufgabe 1

Aufgabe

 Aufg. 36: Erläutere zum KV-Diagramm

Wenn du die geeignete Beschriftung verstanden hast, dann weisst du auch, was jeweils die richtige Stelle ist.

Erläutere den anderen Mitgliedern deiner Lerngruppe:
Die erste Null ganz oben aus der Ergebnisspalte der Wahrheitstafel befindet sich an welcher Stelle im KV-Diagramm?

Jetzt werden Blöcke aus Einsen gebildet.

Die Blockgrößen müssen sich dabei an den 2er-Potenzen orientieren: 8, 4, 2 oder 1.
Je größere Blöcke man bilden kann, desto besser!
Am Ende müssen alle Einsen in mindestens einem Block enthalten sein. Die Nullen bleiben komplett unberücksichtigt.

Ein 8er-Block ist nicht möglich.
Es bietet sich aber ein 4er-Block in der rechten Diagramm-Hälfte an:

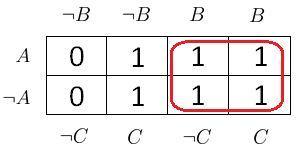
Wie man sieht: in diesem 4er-Block gilt überall $B$.

Jetzt folgen noch zwei 2er-Blöcke:

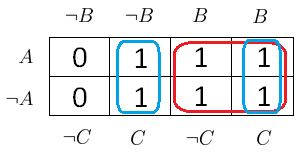
Wie man sieht: in beiden 2er-Blöcken gilt jeweils $C$. (Eigentlich handelt es sich hier wieder um einen 4er-Block, aber die Beschriftung von $C$ an den Spalten des Diagramms lässt keinen zusammenhängenden 4er-Block zu.)

Alle Einsen sind damit in Blöcken gruppiert.
Jede Eins steckt in einem Block in dem $B$ oder $C$ gilt.

Insgesamt erhalten wir damit als einfachste Gestalt: $B\vee C$.

Es gilt also die Äquivalenz:

$((A\to B)\to (B\to C))\to C\equiv B\vee C$

Aufgabe 2

Aufgabe

 Aufg. 37: Kein 8er-Bock?

Oben im Text steht:
"Ein 8er-Block ist nicht möglich."

Erläutere:
Warum ist kein 8er-Block möglich?

Aufgabe 3

Aufgabe

 Aufg. 38: Entweder - oder

Oben im Text steht:
"Jede Eins steckt in einem Block in dem $B$ oder $C$ gilt."

Erläutere:
Warum wurde hier nicht stattdessen geschrieben:
"Jede Eins steckt in einem Block in dem entweder $B$ oder $C$ gilt."

Aufgabe 4

Aufgabe

 Aufg. 39: Warum lieber große Blöcke beim KV-Diagramm?

Oben im Text steht:
"Je größere Blöcke man bilden kann, desto besser!"

Erläutere:
Warum sind größere Blöcke besser?

Aufgabe 5

Aufgabe

 Aufg. 40: Ermittle die einfachste Gestalt unter Zuhilfenahme eines KV-Diagramms!

$A$	$B$	$C$	Einfachste Gestalt?
$0$	$0$	$0$	$1$
$0$	$0$	$1$	$0$
$0$	$1$	$0$	$1$
$0$	$1$	$1$	$0$
$1$	$0$	$0$	$1$
$1$	$0$	$1$	$0$
$1$	$1$	$0$	$1$
$1$	$1$	$1$	$0$

(Du musst das KV-Diagramm auch selber zeichnen und die Zeilen und Spalten auch selber geeignet beschriften.)

Aufgabe 6

Aufgabe

 Aufg. 41: Ermittle die einfachste Gestalt unter Zuhilfenahme eines KV-Diagramms!

$A$	$B$	$C$	Einfachste Gestalt?
$0$	$0$	$0$	$1$
$0$	$0$	$1$	$1$
$0$	$1$	$0$	$1$
$0$	$1$	$1$	$1$
$1$	$0$	$0$	$0$
$1$	$0$	$1$	$1$
$1$	$1$	$0$	$0$
$1$	$1$	$1$	$1$

(Du musst das KV-Diagramm auch selber zeichnen und die Zeilen und Spalten auch selber geeignet beschriften.)