6.2.9.1 Beweisführung anhand einer Wahrheitstafel
Beweisführung anhand einer Wahrheitstafel
Eine Aufgabe und deren Lösung:
Aufgabe
Beweise mit Hilfe einer Wahrheitstafel:
Das folgende Video zeigt die Beweisführung:
Hier ist die im Video erstellte Wahrheitstafel:
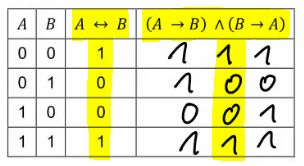
Da beide gelb markierten Spalten identische Werte in den jeweiligen Zeilen aufweisen, ist die Äquivalenz bewiesen. (Unter der Voraussetzung, dass die ermittelten Werte in der Wahrheitstafel korrekt sind.)
Jetzt bis du dran:
Aufgabe 1
Aufgabe
Aufgabe 2
Aufgabe
Aufgabe 3
Aufgabe
Aufgabe 4
Aufgabe
Aufgabe 5
Aufgabe
Aufgabe 6
Aufgabe
Aufgabe 7
Aufgabe